Control del daño en edificios con un primer piso blando ante terremotos impulsivos

Terremotos históricos han demostrado el poder destructivo de estos fenómenos, siendo los más recientes un claro ejemplo de los estragos que aún pueden causar en las sociedades modernas de hoy. Por ello es importante proyectar adecuadamente las nuevas estructuras y actuar sobre las existentes a fin de mitigar el riesgo sísmico que puedan representar ante terremotos severos.

No existe una única forma de evaluar el potencial de daño de un movimiento sísmico, siendo la ductilidad por desplazamiento (displacement ductility) un parámetro típico empleado para medir o limitar el daño en las estructuras [1]. Sin embargo, este factor no toma en cuenta el daño acumulado que se da como resultado de las deformaciones cíclicas alternadas. El daño estructural es una combinación de deformación máxima aparente y deformaciones plásticas acumuladas.

Una forma de relacionar las deformaciones plásticas acumuladas con deformación (plástica) máxima aparente es mediante el parámetro que en la literatura se conoce con el nombre de número de excursiones plásticas equivalentes, n_eq, y que está directamente relacionado con otro concepto (a veces empleado erróneamente como sinónimo) de número de ciclos equivalentes. El número de excursiones plásticas equivalentes se define como la energía W_p disipada por una estructura mediante deformaciones plásticas cuando se somete a un movimiento sísmico dividida por el producto de la carga de fluencia QY y la deformación plástica máxima aparente (igual a la deformación máxima U menos la deformación de fluencia U_Y), ilustrada mediante el área rayada de la Figura 1, donde μ=U/U_Y. Por conveniencia se suelen emplear las ratios η=W_P/(Q_YU_Y), y μ_m=(U-U_Y)/U_Y, y con ellos n_eq es simplemente n_eq= η/μ_m. El número de ciclos equivalentes se define como el número de ciclos de amplitud igual a la deformación plástica máxima aparente necesarios para disipar la cantidad de energía Wp en un sistema ideal elástico perfectamente plástico, y es por ello igual a n_eq/4.

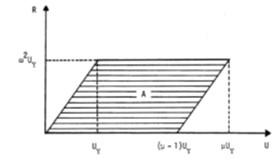
Figura 1:Energía disipada en una excursión plástica de amplitud máxima. Fuente: Zahrah y Hall [1]

El número de excursiones plásticas equivalentes o su equivalente en número de ciclos equivalentes es un parámetro útil para evaluar la habilidad de la estructura para disipar la demanda de disipación de energía de deformación plástica que impone un terremoto. Es decir, cuanto mayor es el número de excursiones plásticas equivalentes, menor es el desplazamiento máximo aparente que debe experimentar para disipar dicha energía. A la inversa, se puede decir también que cuanto mayor es ηeq mayor es la cantidad de energía que la estructura puede disipar mediante deformaciones plásticas para una deformación máxima aparente determinada.

Por otra parte, a mediados del siglo XX Housner [2] en los Estados Unidos y Akiyama ( [3], [4]) en Japón establecieron las bases del diseño sísmico de estructuras basado en el balance de la energía. En la ecuación fundamental de la metodología de proyecto sismorresistente basada en el balance de energía, el término W_p representa la energía de deformación plástica acumulada en la estructura. A diferencia de la deformación elástica que desaparece al eliminar la carga, la deformación plástica permanece y se va acumulando monótonamente hasta alcanzar la situación de colapso. En este sentido, la deformación plástica acumulada o la energía de deformación plástica acumulada es el mejor indicador del daño en la estructura [5].

Los reportes de algunos de los mayores terremotos ocurridos en el decenio de los años 90, tales como Northridge (1994) y Hyogoken-Nanbu (1995) demuestran que los daños catastróficos se atribuyen en muchos casos al desarrollo de un primer piso blando (soft first story). El comportamiento de esta tipología estructural ha sido ampliamente estudiada y sobre ello se puede consultar una publicación relativamente reciente en este blog.

Una forma de predecir adecuadamente el desplazamiento máximo que experimentaría una estructura de este tipo cuando se refuerza mediante disipadores de energía de tipo histerético y se somete a terremotos de campo cercano, es empleando valores apropiados del parámetro n_eq, y que depende, además de las características de la estructura, de la impulsividad del movimiento del suelo.

Akiyama [3] investigó el valor de n_eq para sistemas estructurales genéricos que combinan en paralelo en cada planta i un elemento elástico con uno elastoplástico, y propuso unas expresiones de diseño simplificadas para la ratio i/mi que dependen de la ratio de resistencia r_qi entre la fuerza máxima que desarrolla el elemento elástico y la resistencia del elemento elastoplástico. Estas expresiones son distintas dependiendo de la ley histerética que sigue el elemento elastoplástico, por ejemplo, la fuerza recuperadora exhibe una degradación de resistencia (modelo de Clough).

La expresión propuesta por Akiyama tiene el inconveniente de no tomar en cuenta la influencia de parámetros sismológicos ni el tipo de movimiento sísmico (por ejemplo, lejano o cercano a falla) en la ratio η/μ_m. Este último aspecto fue investigado por Manfredi y otros [6] utilizando sistemas de un grado de libertad elásticos perfectamente plásticos y propusieron estimar n_eq a partir de una expresión que depende de unos parámetros que son: T_NH que es el período inicial de la región de períodos medios en la representación espectral de Newmark y Hall y f_T1 es el período fundamental de la estructura principal (sin disipadores); ID es un parámetro sismológico [7] expresado en función de la aceleración máxima del acelerograma (PGA) y la velocidad pico del suelo (PGV); R que es un factor de reducción definido como la relación entre el producto de la masa (m) de un sistema de un grado de libertad y la aceleración espectral (Sa) dividido por la resistencia del sistema completo (Q_y). En dicha expresión, los parámetros c_1,n, y c_2,n, adquieren distintos valores en función de si la estructura está sometida a un terremoto de campo lejano o de campo cercano.

En una publicación reciente se aborda la protección de edificios con un primer piso blando por medio a su refuerzo empleando disipadores de energía [8]. Para ello se investiga y propone una nueva expresión para calcular n_eq cuando se emplean métodos energéticos, que toma en cuenta la impulsividad del terremoto y por tanto la proximidad de la estructura a la fuente sísmica. En el presente artículo se aportan más detalles en relación a la expresión propuesta.

Para llegar a la referida expresión, se estudian prototipos de estructuras de hormigón armado de 3(N3), 6(N3) y 9(N3) plantas que se refuerzan mediante disipadores de energía de tipo histerético y se someten a 20 registros impulsivos [9]. Estos registros se escalan hasta ajustar (cumpliendo con una tolerancia de ±2%) el input de energía que contribuye al daño (expresado en forma de velocidad equivalente mediante VD) empleada en el dimensionado de los disipadores, siendo ésta 1.08, 0.97 y 0.93 m/s para los prototipos N3, N6 y N9 respectivamente.

Los resultados de esta investigación demuestran que la solución de reacondicionar sísmicamente edificios con planta baja blanda mediante disipadores histeréticos es adecuada no sólo para terremotos lejanos a falla, sino también para terremotos cercanos a falla. Con esta solución se puede aumentar el nivel de protección sísmica en la estructura, y es posible predecir el desplazamiento máximo que ésta experimentaría ante terremotos impulsivos empleando valores adecuados de n_eq.

Para continuar con el propósito de este artículo, se toman los resultados de los análisis dinámicos directos y se estudia la relación entre los parámetros η y μ_m calculados conforme a como se indicó en [8]. La representación conjunta de los resultados se muestra en la figura 2.

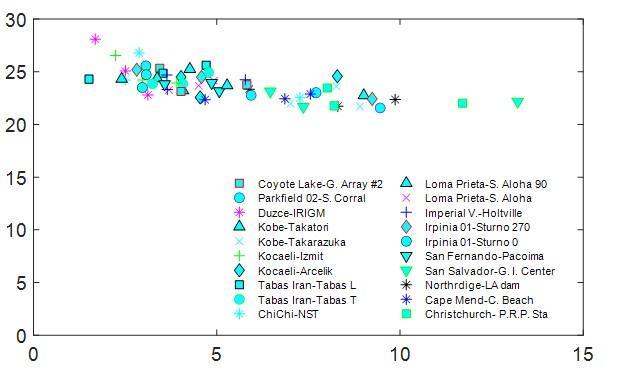
Figura 2: η y μ_m. En esta gráfica y siguientes el subíndice 1 hace referencia a la planta 1.

η es la expresión adimensional de Wp, con lo cual, si nos fijamos en la Figura 2 es fácil concluir que estamos ante valores similares de energía de deformación plástica normalizada en la estructura con disipadores (en su mayor parte en el rango 23 ≤ η ≤ 26). En la Figura 2 también se observa que los valores más bajos de η están asociados a los valores más grandes de μ_m.

Una forma de explicar este comportamiento es por medio a la representación que se hace en la Figura 3. En ella se representa, para cada prototipo de estructura, la relación η/μ_m= n_eq versus el desplazamiento máximo, δ_max1, que ha experimentado la estructura al verse sometida a un terremoto impulsivo. En la gráfica también se representa el n_eq de diseño según la propuesta genérica de Akiyama y la predicción de desplazamiento máximo hecha a partir de ese n_eq de diseño.

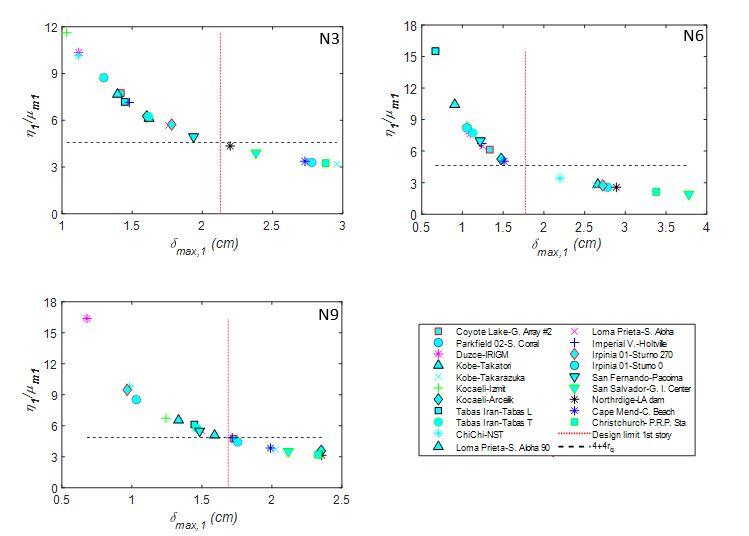
Figura 3: Representación n_eq versus el desplazamiento máximo δ_max1.

En las gráficas de la Figura 3, las relaciones η/m por debajo de la línea negra (que corresponde a la expresión de Akiyama n_eq=4+4r_q), están asociadas a una predicción del desplazamiento máximo del lado de la inseguridad.

La no correspondencia con lo expuesto se debe a que, los terremotos de campo cercano suelen concentrar la demanda de energía en uno o unos pocos pulsos [10]. En términos del n_eq esto significa que la estructura tiene que disipar la misma cantidad de input energía (para este caso 21<η< 29) con un menor número de ciclos de mayor amplitud en comparación con los terremotos de campo lejano. En otras palabras, los terremotos impulsivos demandan mucho desplazamiento en pocos ciclos.

Bibliografía

[1] T. F. Zahrah y W. J. Hall, «Earthquake energy absorption in SDOF structures.,» Journal of Structural Engineering, pp. 1757-1772, 1984.

[2] G. Housner , «Limit design of structures to resist earthquakes,» de In Proceedings of the 1st World Conference on Earthquake Engineering, Berkeley, CA, USA, 1956.

[3] H. Akiyama, Earthquake-resistant design method for buildings based on energy balance, Tokio: Gihodo Shuppan Co., Ltd, 1999.

[4] H. Akiyama, Earthquake-resistant limit-state design for buildings, Tokio: University of Tokyo Press, 1985.

[5] H. Akiyama, Metodología de proyecto sismorresistente de edificios basada en el balance energético, Tokio, Japón: Editorial Reverte, S.A., 2003.

[6] G. Manfredi, M. Polese y E. Cosenza, «Cumulative demand of the earthquake ground motions in the near source,» Earthquake Engineering and Structural Dynamics, vol. 32, pp. 1853-1865, January 2003.

[7] G. Manfredi, «Evaluation of seismic energy demand,» Earthquake Engineering and Structural Dynamics, vol. 30, pp. 485 – 499, July 2001.

[8] S. Mota-Páez , D. Escolano-Margarit y A. Benavent-Climent, «Seismic Response of RC Frames with a Soft First Story Retrofitted with Hysteretic Dampers under Near-Fault Earthquakes,» Appl. Sci., vol. 11, nº 1290, 2021.

[9] «PEER Ground Motion Database,» [En línea]. Available: https://ngawest2.berkeley.edu/.

[10] D. Yang y . J. Zhou, «A stochastic model and synthesis for near-fault impulsive ground motions,» Earthq. Eng. Struct. Dyn., vol. 44, p. 243–264, 2015.