Método de Elementos Finitos y Funciones de Interpolación
La noción base del Método de Elementos Finitos (MEF) es encontrar una solución de un problema complejo a través de la sustitución del problema inicial por varios problemas de simple resolución.
Para lograr esto se discretiza el problema inicial en varios elementos de dimensión reducida, llamados “elementos finitos”. Los elementos finitos son definidos a través de NODOS, que son puntos donde una solución aproximada puede ser adoptada y donde las ecuaciones de equilibrio pueden ser establecidas. A su vez, dado el desconocimiento de los campos de desplazamientos y tensiones, se asume que su variación dentro de los elementos finitos puede ser aproximada por funciones simples, llamadas “funciones de interpolación”.
Procedimiento de Análisis y Caracterización de la Estructura
Los valores nodales de los campos variables son conocidos después de la resolución de las ecuaciones de equilibrio. Entonces las funciones de interpolación son utilizadas para describir el comportamiento de los NODOS de la estructura.
La estructura puede ser caracterizada como: estructura reticulada, losa, cáscara, sólido tridimensional, etc. Se realiza una discretización en varios elementos de dimensión reducida. La interacción entre los elementos se hace a través de un numero finito de puntos, los puntos nodales. Las incógnitas del problema son los desplazamientos de los puntos nodales.
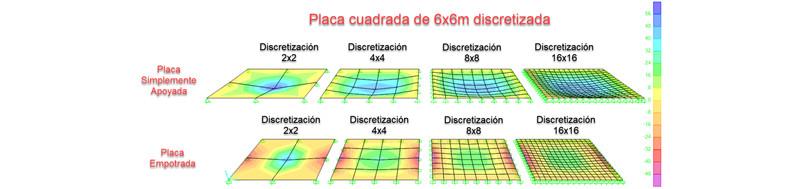
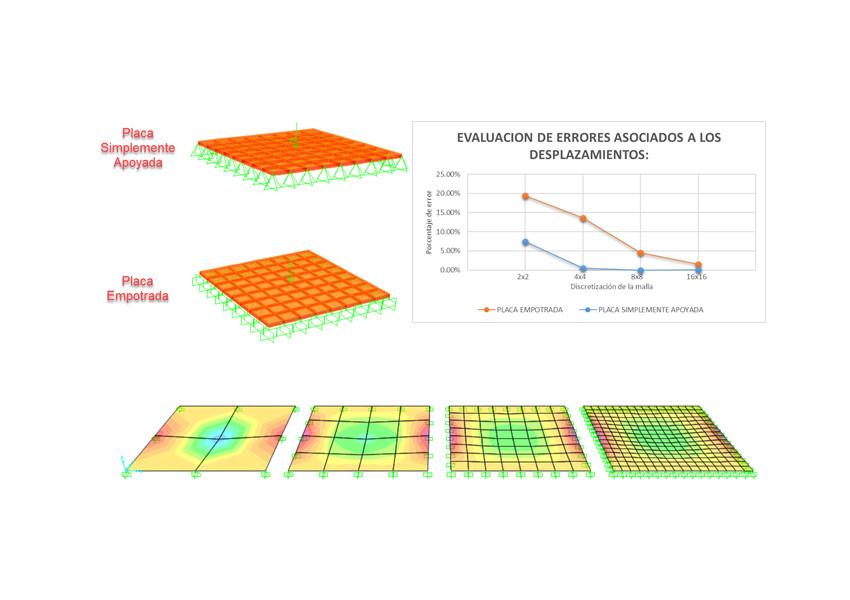
Discretización de placa cuadrada y sus condiciones de apoyo
En el interior del elemento se admite una aproximación de variables fundamentales del problema con base en las funciones de interpolación o funciones de forma. En el caso de la formulación por desplazamientos, estos son obtenidos en términos de las funciones de interpolación, de los valores de los desplazamientos nodales y de la matriz de deformación, que se calcula a partir de las derivadas de las funciones de interpolación. Finalmente, la aplicación del Principio de los Trabajos Virtuales permite determinar la matriz de rigidez del elemento y establecer las ecuaciones de equilibrio, relacionando las fuerzas nodales con los desplazamientos nodales.
Utilizando la matriz de rigidez global de la estructura y relacionando el vector de desplazamientos nodales con el vector de las fuerzas exteriores aplicadas, se pueden establecer las ecuaciones de equilibrio global. Esta matriz global, a su vez, es obtenida a partir de las matrices de rigidez elementales.
Determinación de Desplazamientos y Tensiones
La solución del sistema de ecuaciones lineales, que representa el equilibrio de la estructura, permite determinar el vector de los desplazamientos nodales.
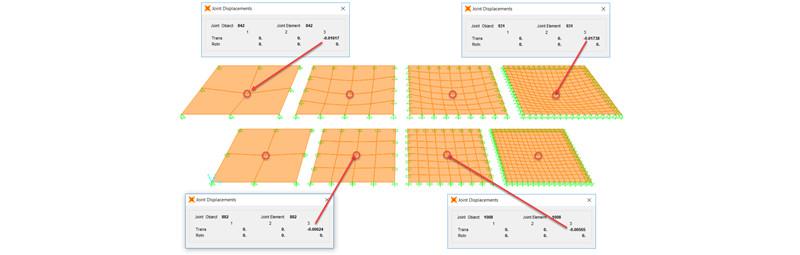
Desplazamientos obtenidos en SAP2000
Validación Analítica del Software de Cálculo
Para la validación de los resultados del programa de cálculo, se utilizan soluciones analíticas conocidas planteadas en “Theory of plates and shells” de autoría de S. Timoshenko y S. Woinowsky-Krieger. Estas soluciones analíticas permiten evaluar el error asociado a la discretización y comparar el desempeño de los diversos tipos de malla de elementos finitos. Los resultados a validar corresponden a DESPLAZAMIENTOS y MOMENTOS (esfuerzos de flexión).
Solución Analítica: Formulación de Timoshenko
El porcentaje de error obtenido a través del programa de cálculo SAP 2000 es calculado mediante la siguiente expresión:
%error=(VSAP2000-Vanalítico)/VSAP2000*100
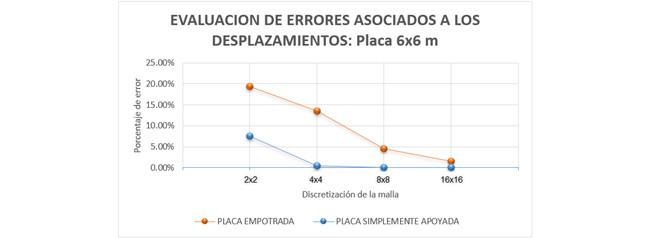
Este chequeo es importante ya que el tamaño de los elementos tiene influencia significativa en la convergencia de la solución, entonces, con un mayor nivel de discretización, la solución tiende a ser más precisa (más próxima a la solución analítica), con porcentajes de error entre 0 y 1%. En la fig. 3 puede apreciarse como para el caso de estudio utilizado, tanto para placas empotradas como simplemente apoyadas de 6X6 metros, a medida que se incrementa la discretización del elemento, al comparar los resultados del software con los de la formulación de Timoshenko, el porcentaje de error tiende a cero.

Evaluación de errores asociados a los desplazamientos: Placa 6×6 m