Descripción del método.
El método de bielas y tirantes es utilizado para el diseño estructural de ciertas regiones de un elemento donde no es aplicable la hipótesis de Bernoulli-Navier que establece que las secciones transversales planas permanecen planas al deformarse. Dichas regiones son llamadas “regiones D” y representan tramos de discontinuidad, ya sea por cambios bruscos de sección, presencia de cargas concentradas o ambas condiciones.
El método busca modelar las regiones D por medio de armaduras o reticulados hipotéticos, compuestos por puntales de concreto comprimido y tensores de acero traccionado representando el estado de las tensiones o esfuerzos en el tramo de elemento analizado bajo un estado de carga dada.
Aplicación del método para el diseño de un cabezal de puente.
Se presenta la aplicación del método en el diseño de un cabezal de puente aplicando los requisitos de diseño del código ACI318-19.
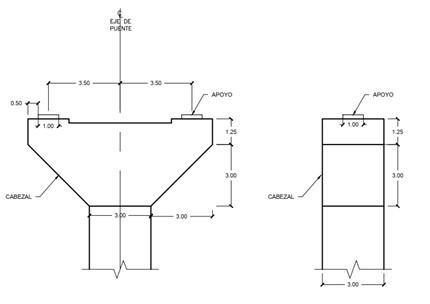
Figura 1. Geometría del cabezal
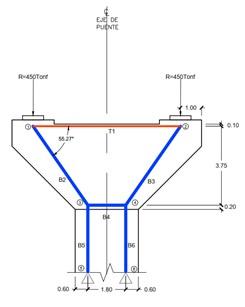
Figura 2. Armadura propuesta.
Para la selección de la armadura se deben tener en cuenta las recomendaciones siguientes: Primero el modelo debe estar en equilibrio con las cargas factoradas, la resistencia de puntales, tensores y zonas nodales debe ser igual o mayor a las fuerzas presentes en dichos miembros, las bielas no se deben cruzar ni superponer, los tirantes pueden cruzar otros tirantes o bielas y el menor ángulo entre puntales y tensores unidos en un nodo será de 25°.
Para comprobar la elección de la armadura pueden utilizarse modelos bidimensionales, en los que puedan visualizarse las trayectorias de los esfuerzos. Lo que se busca es que los puntales y tensores sean lo más representativos posible. El modelo bidimensional se presenta más adelante y también la comparación en los comentarios finales.
Para este análisis, las propiedades de los materiales utilizados son: concreto f’c=280 kgf/cm2, acero de refuerzo grado 60 fy=4,200 kgf/cm2.
La solución del modelo es la siguiente:
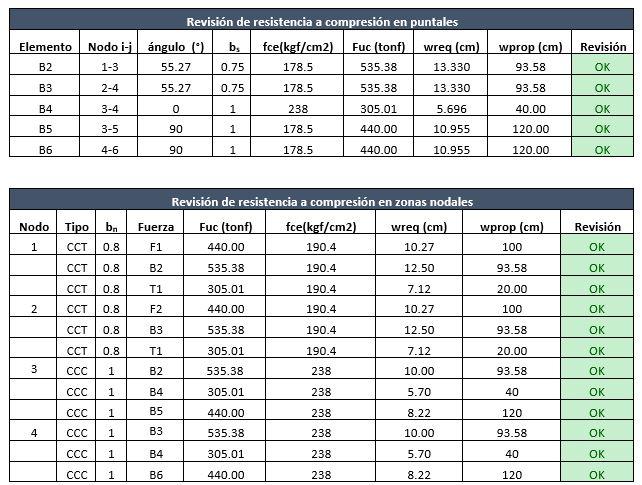
Dónde: fce es la resistencia a compresión en puntales o nodos, Fuc es la fuerza del miembro analizado, wreq es el ancho requerido para resistir la fuerza aplicada y wprop es el ancho conforme a la geometría propuesta.

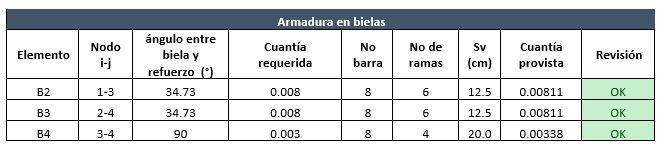
Modelo matemático bidimensional.
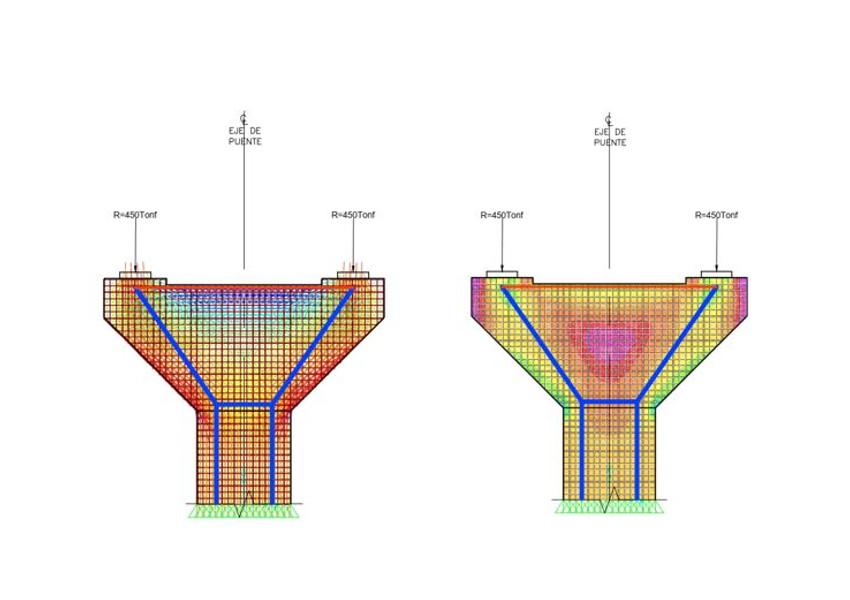
Se creó un modelo de elementos finitos con placas tipo membrana y se aplicó la carga ultima, se muestran las trayectorias de esfuerzos, esfuerzos Von Mises y el acero requerido en la zona a tensión.
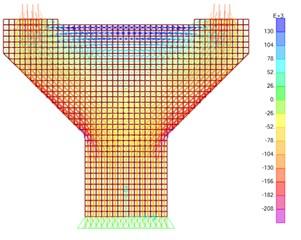
Figura 3. Esfuerzos máximos y mínimos representados como flechas en kgf/m2
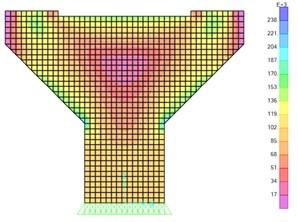
Figura 4. Esfuerzos von Mises kgf/m2
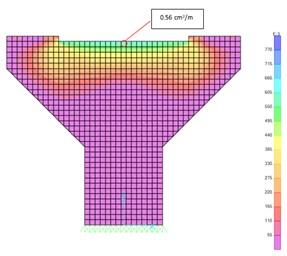
Figura 5. Acero requerido en modelo bidimensional Ast1 en la cara top.
El acero total se obtiene al multiplicar por las dos caras y un ancho de 100cm que corresponde al ancho unitario de distribución. Ast=0.56cm2/cm*100cm*2=112cm2.
Modelo matemático tridimensional.
Se realiza un modelo por medio de sólidos y se obtienen las representaciones gráficas de la trayectoria de esfuerzos máximos y mínimos (Esfuerzos Von Mises) y a partir de un section cut el área de acero requerido en la zona de tensión en este modelo.
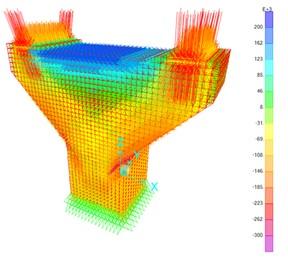
Figura 6. Esfuerzos máximos y mínimos representados como flechas en kgf/m2
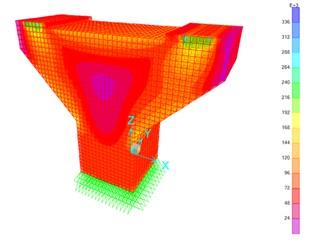
Figura 7. Esfuerzos von Mises kgf/m2

Comentarios.
Puede observarse que con ambos modelos matemáticos se obtienen resultados bastante cercanos al cálculo manual. El modelo bidimensional en este caso es lo suficientemente representativo y requiere menor tiempo de análisis que el modelo tridimensional, además es muy útil para la visualización de trayectorias de esfuerzos y la selección del reticulado hipotético.
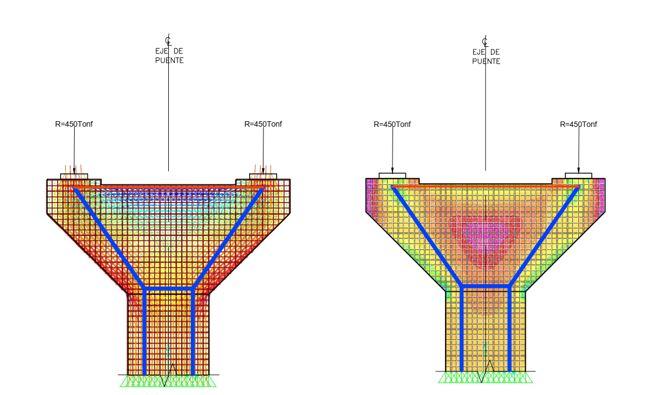
Figura 9. Superposición de reticulado de puntales y tensores y esfuerzos máximos y mínimos representados como flechas a la izquierda y esfuerzos Von Mises a la derecha.