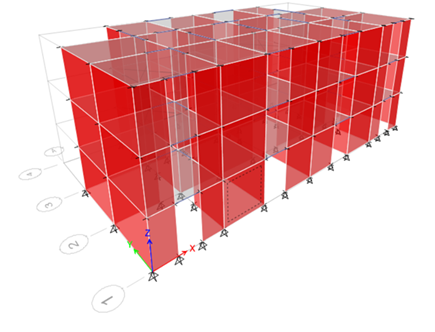
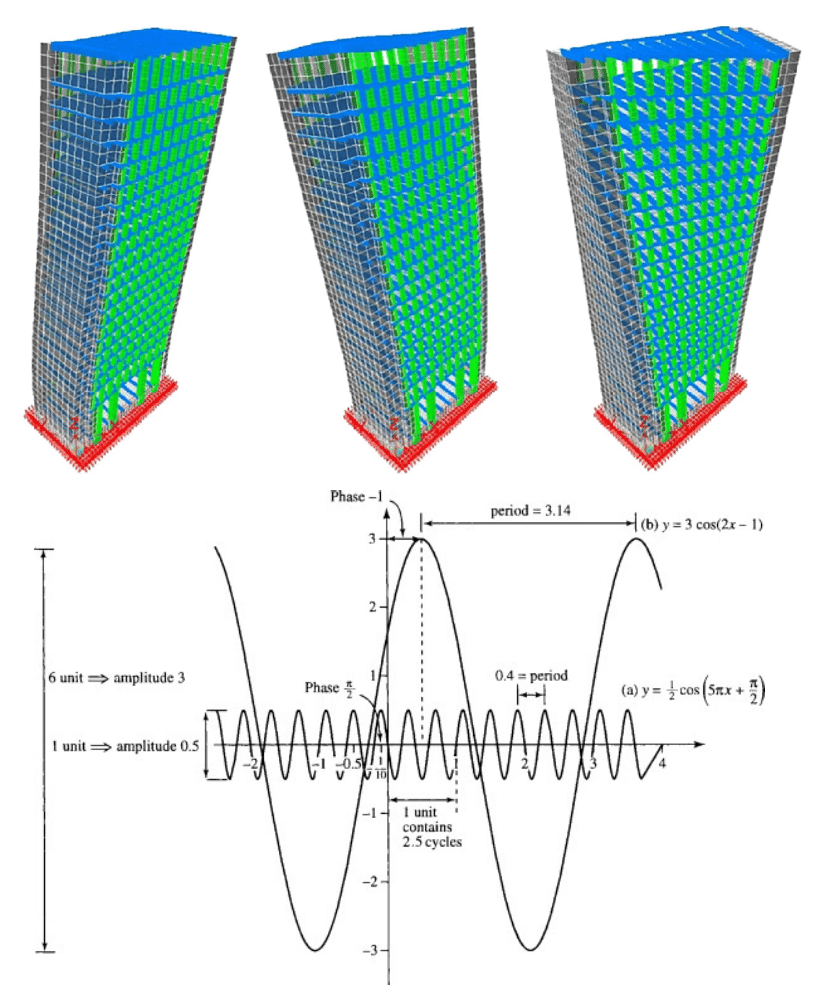
La ingeniería civil actual exige respuestas más rápidas, seguras y precisas ante estructuras cada vez más complejas: puentes con grandes luces, edificios altos expuestos a viento, cimentaciones en suelos heterogéneos o infraestructura crítica operando bajo condiciones extremas.
En este escenario, la simulación numérica se ha convertido en una de las herramientas más valiosas para el ingeniero civil estructural. Permite analizar comportamientos que ya no pueden resolverse con métodos analíticos tradicionales, integrando geometrías complejas, materiales no lineales, múltiples escalas y fenómenos acoplados.
A continuación, presentamos 9 claves esenciales para comprender el camino completo: desde el modelo matemático hasta el enfoque moderno de Digital Twins (gemelos digitales) y simulación basada en datos.
✅ Clave 1: la simulación comienza con un buen modelo matemático
Todo análisis estructural serio parte de un principio: la realidad debe traducirse en ecuaciones.
Un modelo matemático es una representación de un fenómeno real mediante símbolos y relaciones lógicas: variables, parámetros, ecuaciones y condiciones asociadas. En ingeniería estructural esto significa traducir:
- geometría,
- propiedades del material,
- cargas,
- restricciones,
en expresiones que puedan analizarse y simularse.
Lo interesante es que no existe una única forma correcta de modelar: el mismo fenómeno puede representarse con ecuaciones diferenciales ordinarias (EDO), ecuaciones diferenciales parciales (EDP), métodos estadísticos o incluso enfoques basados en machine learning.
✅ Clave 2: los modelos clásicos explican mucho… pero no lo explican todo
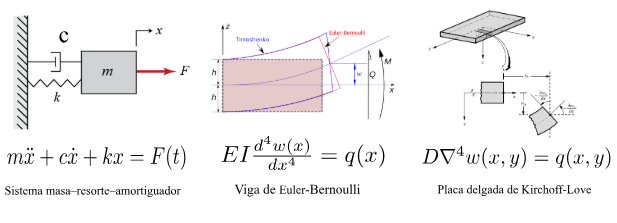
Muchos conceptos base de la ingeniería estructural se entienden con modelos ideales como:
- el sistema masa–resorte–amortiguador,
- la viga de Euler-Bernoulli,
- o la placa delgada de Kirchhoff–Love.
Estos modelos son fundamentales porque enseñan el comportamiento mecánico básico y permiten validar ideas mediante formulaciones conocidas.
Sin embargo, su gran limitación es evidente: asumen simplificaciones que rara vez se cumplen en una estructura real (material perfecto, geometría simple, cargas idealizadas).
✅ Clave 3: en estructuras reales, la solución analítica casi nunca es viable
A medida que un problema se acerca a la realidad, aparecen condiciones que rompen el camino analítico:
- dominios complejos y condiciones de borde no triviales,
- no linealidades materiales (fisuración, plasticidad),
- no linealidades geométricas,
- contacto,
- multiescala,
- acoplamientos (fluido–estructura, térmico–mecánico).
Por eso, ante la clásica pregunta:
¿Las ecuaciones diferenciales tienen siempre solución analítica?
La respuesta es directa: No.
En la práctica, muchos problemas reales de ingeniería civil incorporan geometrías complejas, condiciones de borde no triviales, no linealidades (materiales o geométricas), contacto, e incluso fenómenos acoplados como fluido–estructura o térmico–mecánico. Todo esto rompe el “camino analítico” y hace imposible obtener una fórmula exacta cerrada.
Entonces surge la pregunta clave:
¿Cómo podemos saber cuál es la solución, o al menos aproximarnos a ella?
Aquí aparece el rol esencial de la simulación numérica: en lugar de buscar una solución exacta con lápiz y papel, usamos métodos numéricos para aproximar el resultado dividiendo el problema en partes más pequeñas y tratables (por ejemplo, con una cuadrícula o una discretización), como sucede en la aproximación del área bajo la curva (integrales).
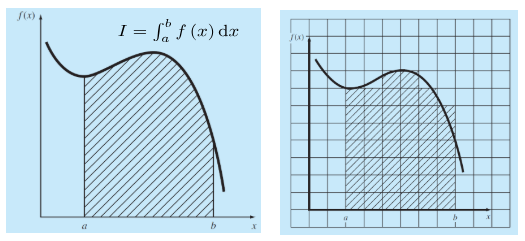
Los métodos numéricos explotan la capacidad del computador para realizar grandes cantidades de operaciones con el fin de reproducir la realidad física dentro del ordenador en forma de números.
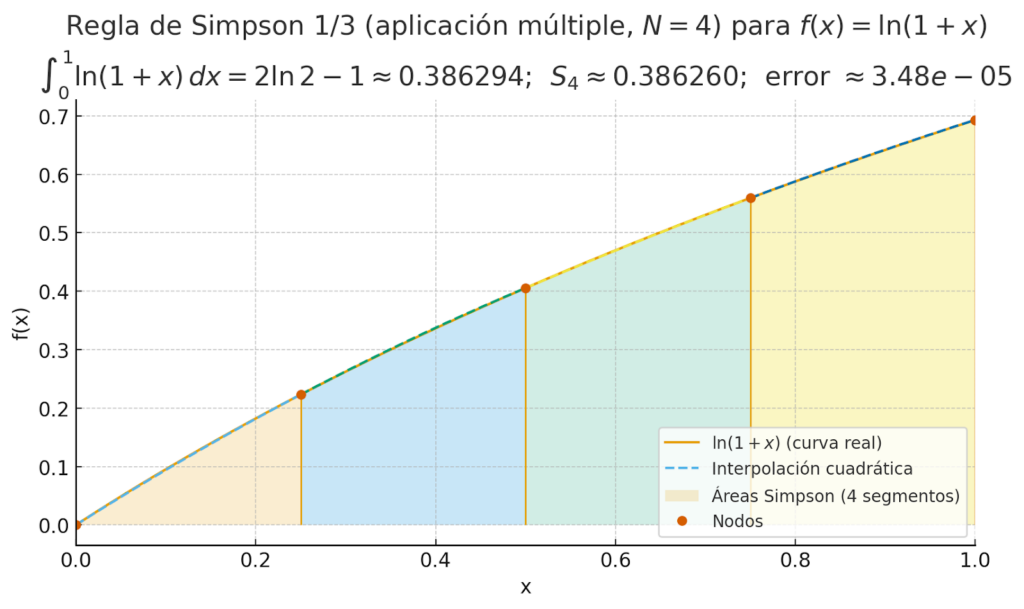
✅ Clave 4: los métodos numéricos son el puente entre la teoría y la ingeniería aplicable
Los métodos numéricos permiten aproximar soluciones cuando no existe una solución cerrada o cuando obtenerla sería impráctico.
La idea central es simple y poderosa: convertir un problema continuo en uno discreto, usando aproximaciones controladas. Por ejemplo, aproximar un resultado teórico usando una cuadrícula o partición que “divide” el dominio para calcular integrales o campos físicos.
Esta lógica es la base de casi toda la simulación moderna.
✅ Clave 5: la computación convierte la simulación en un “laboratorio virtual”
La simulación numérica no sería posible sin el avance computacional.
Como se explica en el material de base, estos métodos aprovechan la capacidad del computador para ejecutar grandes cantidades de operaciones y reproducir la realidad física dentro del ordenador como números.
Hoy esto significa que es posible:
- evaluar múltiples escenarios rápidamente,
- validar hipótesis antes de construir,
- optimizar diseños,
- reducir riesgos,
- ahorrar recursos en obra.
En otras palabras: la simulación es una extensión directa del criterio ingenieril, pero con la potencia de cálculo como aliada.

✅ Clave 6: el Método de los Elementos Finitos (FEM) es el estándar en ingeniería civil
El Método de los Elementos Finitos (MEF o FEM) es la técnica más utilizada para resolver problemas estructurales complejos.
Su lógica es directa:
- Se divide el dominio en pequeñas “piezas” llamadas elementos
- Se conectan mediante nodos
- Se aproxima el comportamiento (por ejemplo desplazamientos) con funciones de forma
- Se ensambla un sistema global (como una matriz de rigidez)
- Se aplican condiciones de borde y cargas
- Se resuelve el sistema para obtener la solución aproximada
Este enfoque permite llevar el análisis desde problemas académicos hasta estructuras reales complejas.

Imágenes cortesía de Compass Ingeniería y Sistemas SA, www.compassis.com
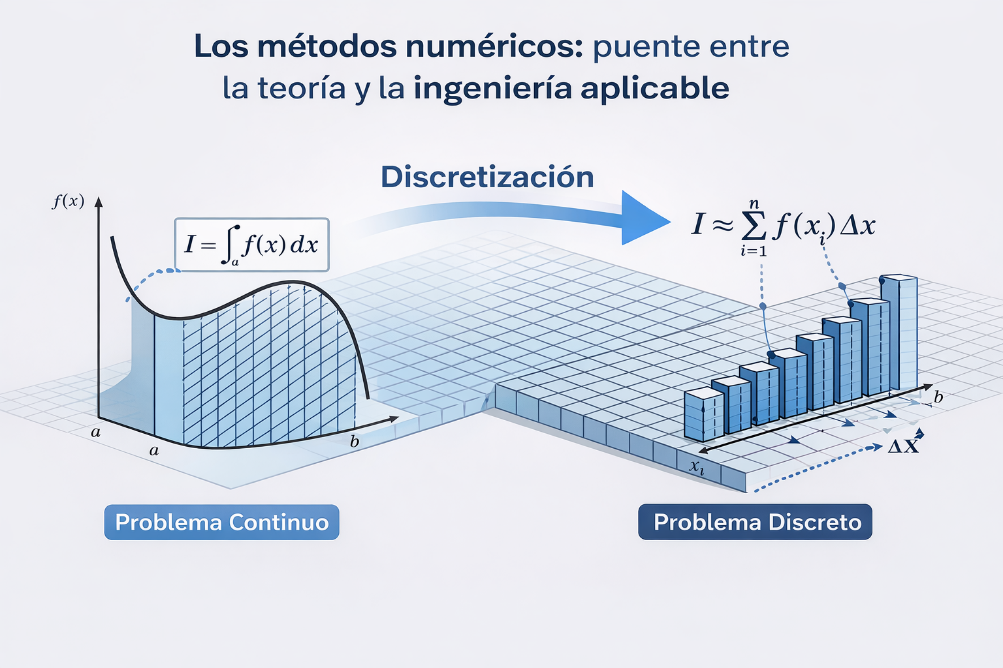
✅ Clave 7: FEM requiere transformar ecuaciones físicas en una formulación “resoluble”
Uno de los puntos más importantes (y muchas veces menos visibles) del FEM es que no se trabaja directamente con la EDP “original”, sino que se transforma en una formulación adecuada para el método.
Se toma como ejemplo la ecuación de Poisson, con sus condiciones de borde, donde el campo incógnita (trial function) es el valor a encontrar.
Para convertir la ecuación diferencial en un problema variacional se aplican pasos como:
- multiplicar por una función de prueba (test function)
- integrar sobre el dominio
- aplicar integración por partes para obtener la formulación débil
Esto permite construir:
- una forma bilineal
- una forma lineal
y resolver el sistema con espacios funcionales apropiados (por ejemplo, espacios de Sobolev).
✅ Clave 8: herramientas modernas (como FEniCSx) aceleran el desarrollo de simulaciones avanzadas
Hoy la simulación numérica no es solo “usar un software”, sino también construir y extender soluciones.
En esa línea, herramientas como FEniCSx permiten definir problemas variacionales FEM mediante código, y seguir un flujo típico:
- identificar dominio, condiciones de contorno y términos fuente
- reformular como problema variacional FEM
- escribir el programa en Python
- ejecutar y visualizar resultados
Este enfoque tiene una ventaja enorme: automatización, trazabilidad y escalabilidad, especialmente útil en proyectos complejos o repetitivos.

✅ Clave 9: el futuro de la simulación está en los datos, HPC y los gemelos digitales
Aunque FEM ya resuelve problemas industriales enormes, el futuro está impulsado por nuevas necesidades: más datos, más velocidad y más integración con el mundo real.
En el contenido se destacan tendencias claras:
🔹 Data Driven
Un enfoque donde las decisiones del modelo se obtienen desde los datos, sustituyendo leyes constitutivas tradicionales por modelos aprendidos (por ejemplo redes neuronales entrenadas).
🔹 Digital Twins (Gemelos Digitales)
Un gemelo digital es un modelo computacional “vivo” de una estructura (puente, edificio, ala…) sincronizado con sensores en el tiempo, útil para diagnóstico, mantenimiento y control.
🔹 HPC (High Performance Computing)
El HPC permite simular con muchos procesadores (CPU/GPU) en paralelo sobre clusters o supercomputadores, logrando tiempos de ejecución muy reducidos para modelos de gran escala.
🔹 Scientific Machine Learning
La tendencia más sólida es combinar modelos basados en física (como FEM) con datos masivos para lograr modelos más predictivos y robustos.

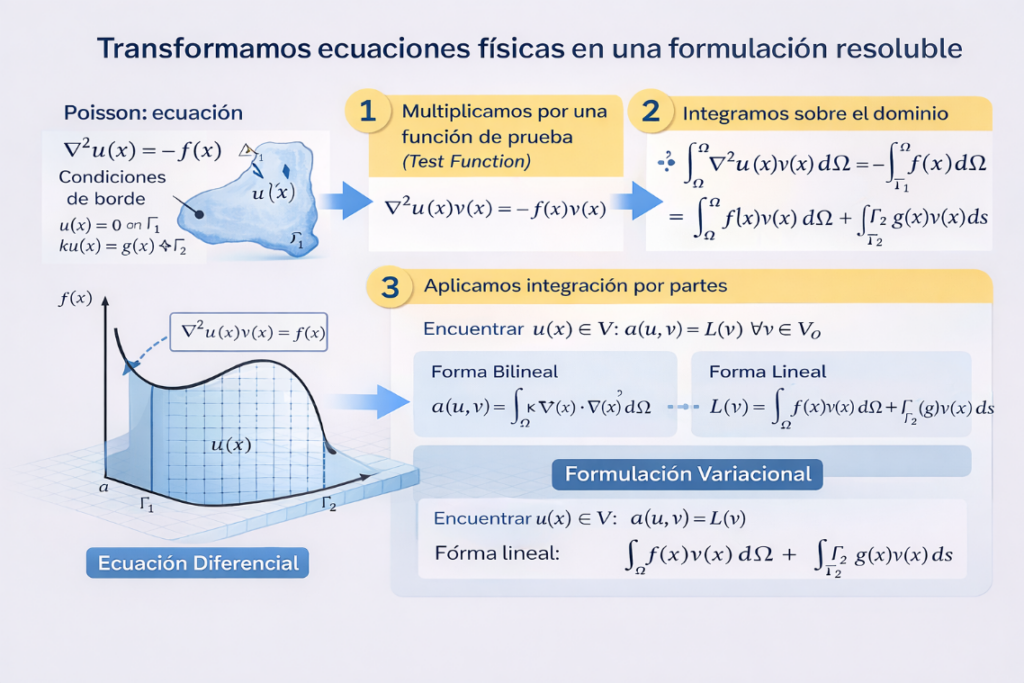
✅ Clave 10: la simulación del futuro apunta a computación cuántica y nuevas fronteras tecnológicas
Aunque el MEF/FEM, los gemelos digitales, el HPC y la simulación basada en datos ya están transformando la ingeniería civil, el futuro sigue avanzando hacia nuevas capacidades computacionales que podrían cambiar por completo la escala de lo que hoy consideramos “simulable”
¿Por qué podría ser relevante para ingeniería civil?
Aún cuando su aplicación industrial está en desarrollo, la computación cuántica promete acelerar ciertos tipos de cálculo que hoy son muy costosos, especialmente en:
- optimización estructural avanzada (diseño con múltiples restricciones y variables),
- problemas inversos (identificar parámetros del modelo desde mediciones),
- modelos probabilísticos y bayesianos con grandes volúmenes de datos,
- simulaciones multiescala donde la demanda computacional crece muy rápido.
Esto significa que en el mediano y largo plazo podríamos ver herramientas capaces de resolver en minutos problemas que hoy requieren horas o incluso días de procesamiento.
Conclusiones: simular mejor es diseñar mejor
La simulación numérica ya no es una herramienta “opcional”. Es un pilar de la ingeniería moderna porque permite:
- representar estructuras complejas con fidelidad,
- reducir incertidumbre,
- evaluar riesgos antes de construir,
- optimizar materiales y costos,
- y evolucionar hacia sistemas inteligentes como los gemelos digitales.
Hoy el camino va desde el modelo matemático, pasando por FEM y computación de alto rendimiento, hasta llegar a enfoques híbridos basados en datos y modelos en tiempo real.
El resultado: una ingeniería civil más precisa, más eficiente y preparada para los desafíos del futuro.
Si quieres especializarte en una temática de alta demanda como esta, puedes inscribirte en nuestra especialización a continuación: